
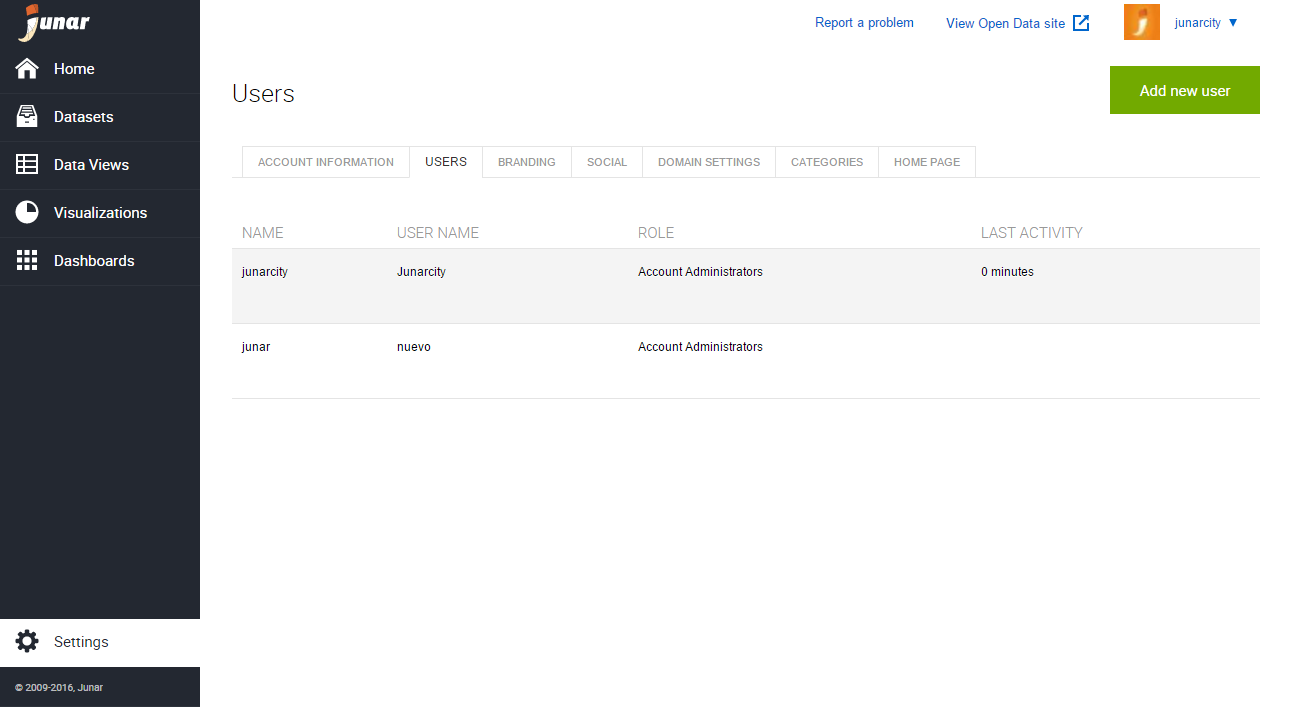
We have also considered the case where x is chosen to be the midpoint xi of the subinterval fx i21, x i g. If we choose x to be the right endpoint, then x x i and we have y 2 b a y 0 b a 1 0 1 2 0 b a f sxd dx Rn n o f sx i d Dx Figure The approximations L n and Rn defined Equations 1 and 2 are called the left endpoint approximation and right endpoint approximation, respectively. If x is chosen to be the left endpoint of the interval, then x x i21 and we have x (b) Right endpoint approximation y (c) Midpoint approximation FIGURE x f sxd dx L n n o f sx i21 d Dx If f sxd 0, then the integral represents an area and (1) represents an approximation of this area the rectangles shown in Figure 1(a). Recall that the definite integral is defined as a limit of Riemann sums, so any Riemann sum could be used as an approximation to the integral: If we divide fa, bg into n subintervals of equal length Dx sb 2 adyn, then we have x y (a) Left endpoint approximation y f sxd dx n o f d Dx where x is any point in the ith subinterval fx i21, x i g. In both cases we need to find approximate values of definite integrals. There may be no formula for the function (see Example 5). For example, it is impossible to evaluate the following integrals exactly: y e x dx y s1 1 x 3 dx 1 y 0 21 The second situation arises when the function is determined from a scientific experiment through instrument readings or collected data.
.jpg)
Sometimes, however, it is difficult, or even impossible, to find an antiderivative (see Section 5). The first situation arises from the fact that in order to evaluate yab f sxd dx using the Theorem of Calculus we need to know an antiderivative of f. Approximate Integration: Trapezoid Rule and Rule There are two situations in which it is impossible to find the exact value of a definite integral. This content is not yet final and Cengage Learning does not guarantee this page will contain current material or match the published product.



 0 kommentar(er)
0 kommentar(er)
